原文来自：The boundary state from open string fields
模糊翻译：即保持原句表达意思，但不追求翻译精度。
这是hep-th上今天最好的文章，是关于弦场论的。
Michael Kiermaier, Yuji Okawa, Barton Zwiebach (PDF)
作者构造了边界态-这是一个根据闭弦态的D-膜的推广态的描述。
如果你认为这个85页的文章太长的话，那么你至少需要知道的公式是（3.14）和（3.18），
在第二个公式里，是L_R和对易子的组合是很自然的，这个对易子是由Psi和B_R构成的梯度对易子（graded commutator）。在一个（“背景无关的”）纯三次（cubic）弦场论中，这两项应该仅仅来自于Psi，纯粹的Psi的三次项，也就是“Q+Psi”项，该项把Q推广到任意背景中。
在第一个公式中，有序路径（path-ordered）指数中，有一个因子“L_0”，这里这个积分围道的选择是什么呢？我相信，对于IQ（智商）低于250的人如果没有经过冗长的计算的话，肯定猜不出来的J。那么让我来说明下，为什么会有两个积分。闭弦态是由闭弦上不同点构成的（闭弦围道积分），每一个点的贡献是把一个点和闭弦上的其它点连接起来——在P中打开围道积分。这种连接是由开弦的演化给出的。
令人非常惊奇的是，这些公式给出了Schnable 规范，这些公式可以用解析方法计算，最终的边界态和我们已知的弦场论解是相吻合的。
至少，这篇文章提高了人们的直接在不同的D-膜位形（或是其推广）描述的变换能力。该文章也提高了我们对开弦场论中的闭弦的理解。这些直接的公式是非常重要的，对于自由度的选择为什么可以这么多（描述同样的弦物理学）这个问题，他们能够减少理论的神秘性。一旦你知道“场重定义”，这两种方法不再是“真正不同的”。
这篇文章中，所有公式都是“切实的”，也就是更正式的：他们可以被展开成弦的振动项，其中所有系数都是有限的，不像某些某些场合有基于启发式描述的误导。
第二篇文章
我想说的今天最好的第二篇文章是第二文章J。是Rolf Schimmrigk写的“应用弦论”，虽然不是很技术化的（也许非典型的写给镜像对称专家的）。他说，弦理论有很多解，这并没有什么坏处：我们知道这点已经几十年了，一个好的理论必须能够描述所有可能的宇宙，而不仅仅是我们的宇宙。
更像以前的物理学的情形，实验数据有助于选择正确的真空，他直接提到宇宙学的，引力的，以及其他的实验限制和未来的观测，将会有助于我们确定正确的真空（或真空的分类）。
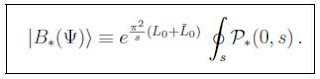
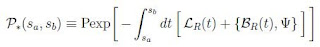
没有评论:
发表评论