我们通常把基本当作零维的对象,比如电子。一个基本的推广就是弦:一维的对象,没有厚度但是有长度,10-33 cm。和我们人类100cm这样的尺度比较,这是一个非常小的长度。因此弦看起来就像点状的粒子。但是弦的本质有一些重要的应用,这是我们即将看到的。
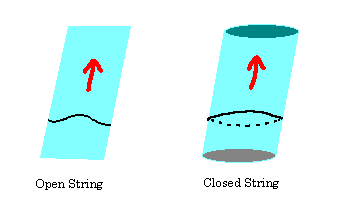
弦分为开弦和闭弦。在时空中移动扫出一个我们想象的面:世界面。

弦有很多的振动模式,这些模式可以由量子数来刻画,比如质量,自旋等等。其基本思想是,这些模式具有一套量子数,这些量子数对应于不同类型的基本粒子。这是最终的统一:所有我们所知的的基本粒子由一个对象描述:弦!(有一个简单的类比,大提琴的弦。不同的声音对应于大提琴的不同的振动,也就是每种粒子对应于弦的不同振动。)
作为一个粒子,我们考虑闭弦的振动模式:

这些模式是自旋为2的无质量的引力子(传递引力的媒介粒子)的刻画。这是弦论的极具有吸引力的一方面。这就很自然的,不可避免的在基本相互作用中包含了引力。
弦的相互作用有分裂和联合。例如:两个闭弦湮灭成一个闭弦,见下图:

注意到相互作用的世界面是一个光滑的面。这本质上解释了弦论的另外一个很好的特性。这样我们就不再为量子场论中的点状粒子产生的无穷大所苦恼。类似于上图,量子场论中的点粒子的费曼图是:

在上图中,相互作用点出现在一个拓扑奇点上(即三线的交点)。这导致在高能的情况下点粒子理论不再适用。
如果我们把两个基本的闭弦相互作用粘合在一起,我们得到一个闭弦相互作用的过程:两个闭弦粘合在一起,称为一个中间态闭弦,然后又分裂成两个闭弦:

这个过程我们称为:树形图相互作用。为了用微扰论计算量子力学幅度,我们需要加入更高阶的量子过程。对于阶数越高,贡献越小的情况,微扰论提供了一种很好的方法。那么我们只需要计算前面几阶就可以得到比较精确的结果。在弦论中,更高阶的图形是对应于世界面中洞的数目。

我们幸运的发现,在微扰论的每一阶中,有且仅有一个图。(在量子场论中,图形的数目是随阶数几何级数增长的。)而坏消息是,世界面有更多的洞的时候,计算需要很复杂的数学。微扰论对于研究弱耦合问题是非常有效的工具,我们当前对于粒子物理学和弦理论大多数理解都基于此。当然这还远远不够。对这些更深层次的问题的解答,我们需要有一个完备的非微软的理论描述。






没有评论:
发表评论